Decision Trees

• Popular representation for interpretable classifiers; even among humans!
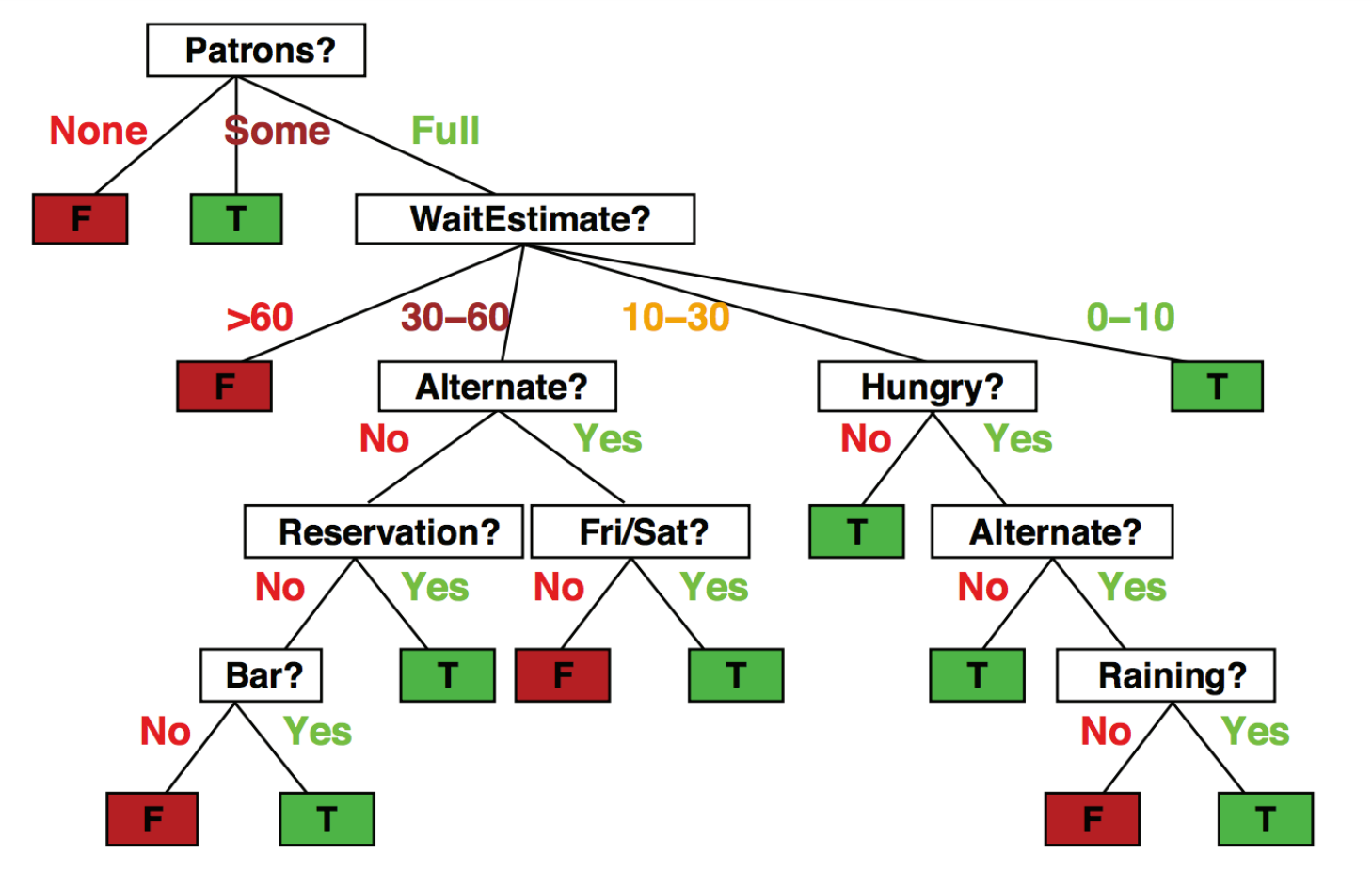
• Example: I’ve just arrived at a restaurant. Should I stay (wait for a table) or go elsewhere?

One may choose to use the following set of rules to make their decision:

source: ai.berkeley.edu

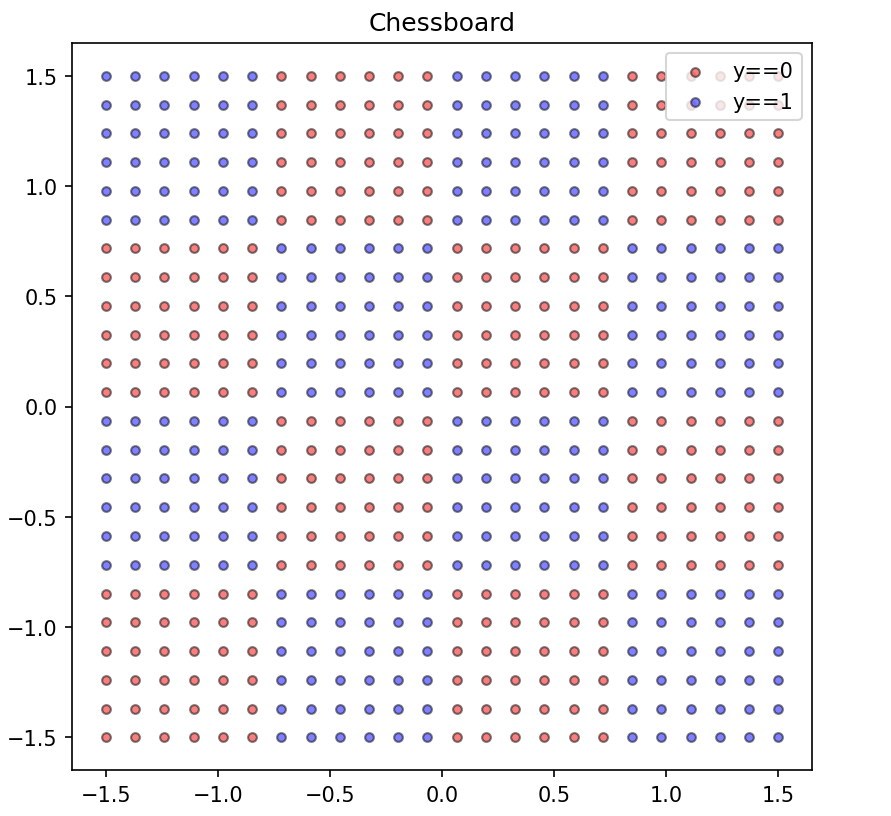
Consider this dataset:

• 4x4 checkerboard dataset with alternating classes
• Red points \(\implies y=0\)
• Blue points \(\implies y=1\)
• Want to model dataset generation rationale

Fit a Decision tree?

The following decision tree is achieved:

Rationale is perfectly captured by a decision tree with depth=7

A twist

(literally)

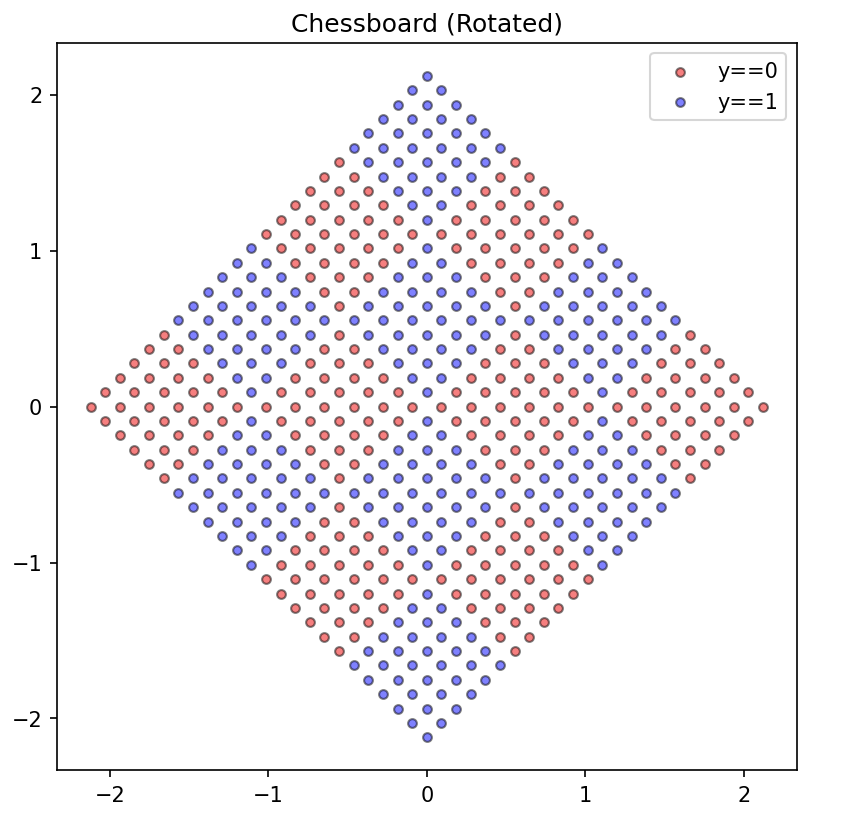
Consider this dataset:

• Previous dataset, rotated by \(45^{\circ}\) from the origin
• How will our decision tree algorithm perform on this dataset?

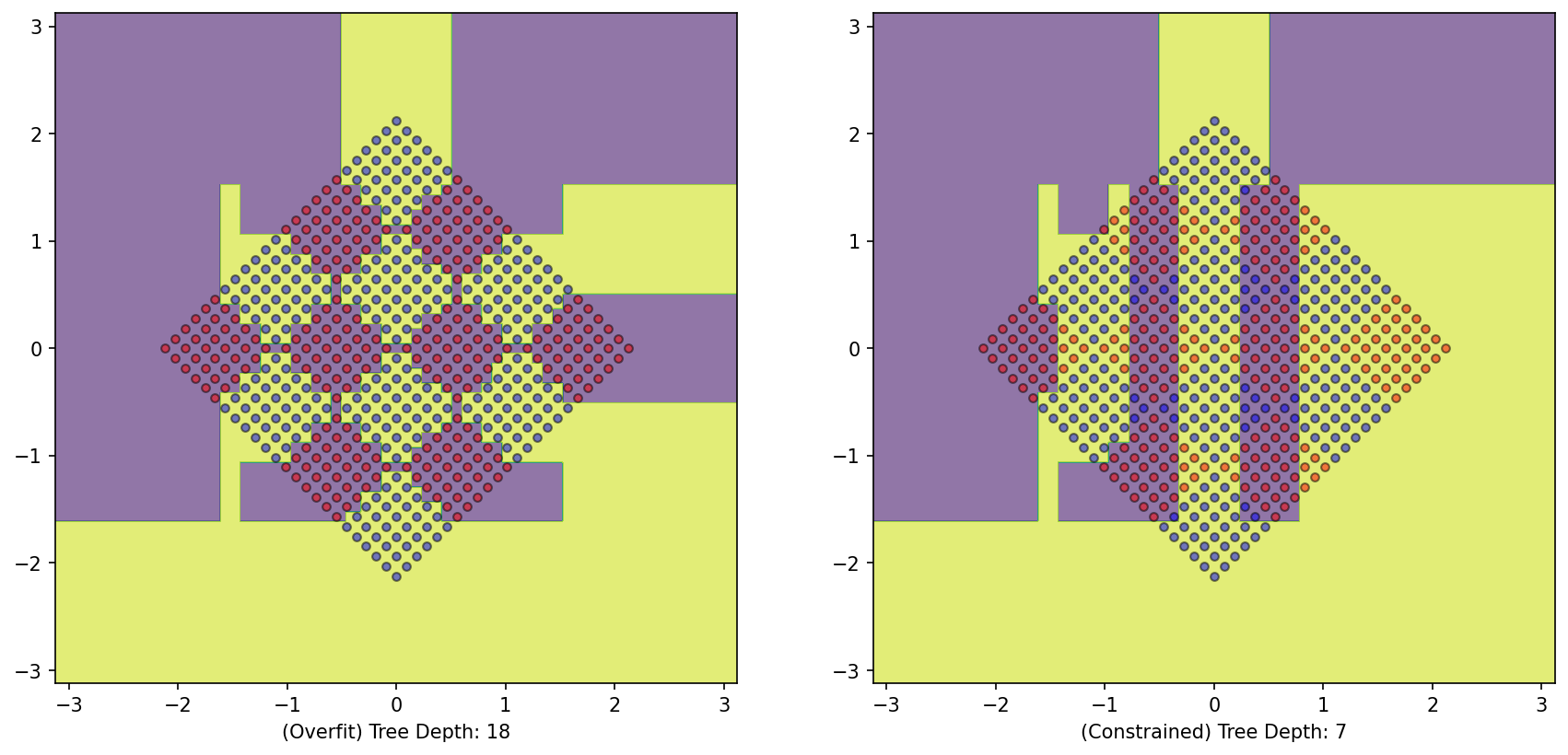
• A complicated decision tree with 18 questions is required
• Note that the depth is not constrained
• Number of corners \(\propto\) density of class
• Unconstrained - Overfitting

• depth=7 found sufficient to capture structure of dataset
• But performance is not invariant to transformation by rotation

Why?

Decision trees make the following presumption about the structure of data:

Can figure class out based on a series of binary questions (yes/no) on individual features

Inductive Bias: Anything which makes an algorithm learn one pattern over another

• Inductive bias of decision trees entails the use of axis-parallel splits to construct the decision boundary
• Sensitive to rotations
• Algorithm invariant to rotation?

K-Nearest Neighbors

• Lazy Human; do not want to learn anything
• Predict on input \(\mathbb{x}\) as follows:
  • Find others who are in a similar situation as \(\mathbb{x}\)
  • Choose the top \(K\) people w.r.t similarity
  • Have them vote on the prediction

In our dataset, we define similarity to be inveresely proportional to the distance between datapoints; i.e

The closer the datapoints, the more similar they are

The following decision boundaries are achieved by the KNN algorithm:

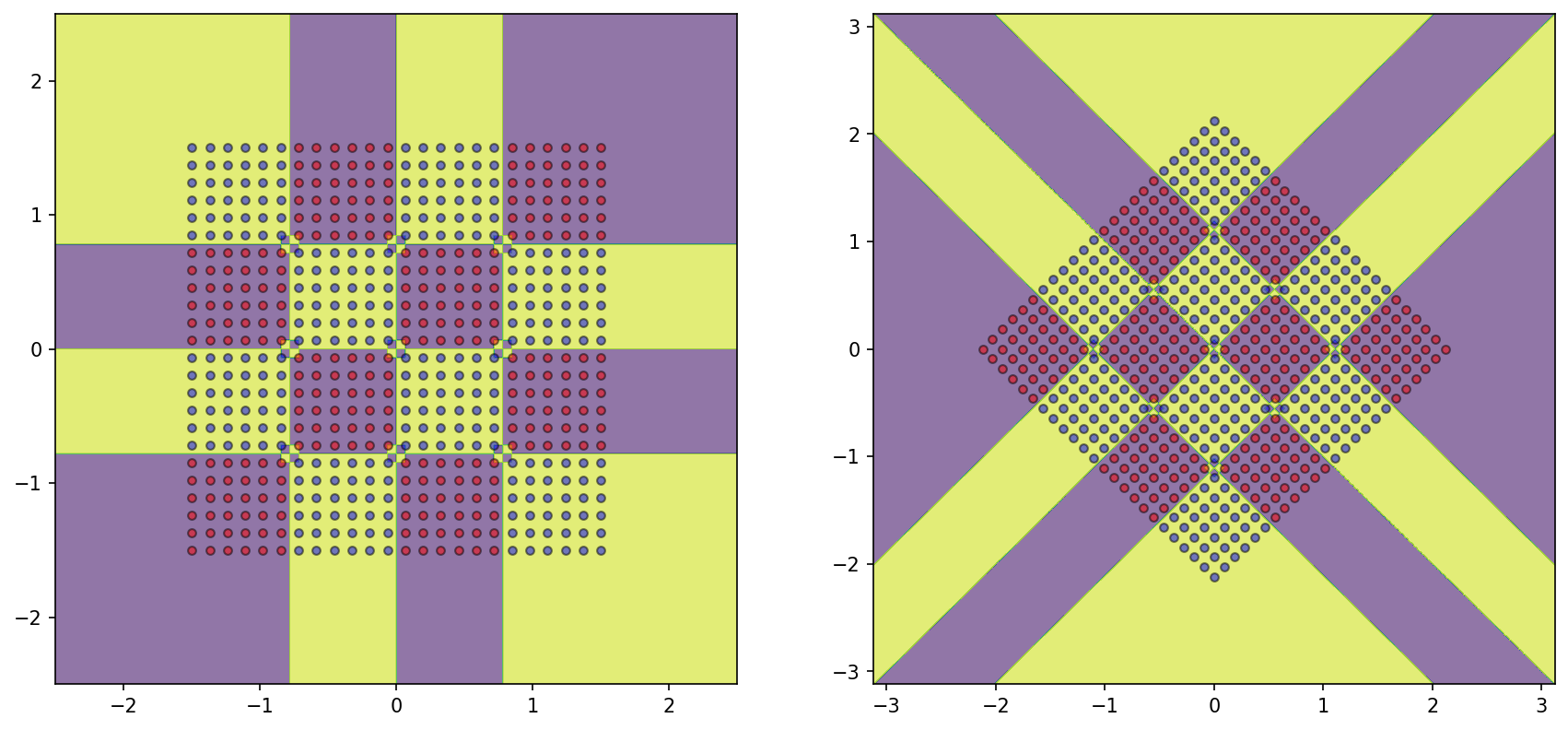
• Rotation has no impact on the decision boundary of KNN!
• Inductive bias for KNN?

Consider the following dataset:

• The dataset is linearly seperable
• Blue points \(\implies\) Class 1, and Red points \(\implies\) Class 2
• Note that the range (and therefore scaling) is vastly different for Features 1 & 2

KNN Results in the following decision boundary:

• Distance is invariant to scaling of features
• Feature 2 is totally neglected during prediction
• Apply StandardScalar?

• KNN has satisfactory performance; but we raise some questions:
  • Is a StandardScalar transformation advisable?
  • Dataset is given to be linearly seperable; Can we do better?