System of equations in two variables

General system

A general system of equations in two variables and two unknowns is given by: \[ \begin{aligned} a_1x + b_1y &= c_1\\ a_2x + b_2y &= c_2 \end{aligned} \]

The slope and the constant term control the whole situation. This system can fall into one of these three categories based on the number of solutions it has:

• no solution
• unique solution
• infinitely many solutions

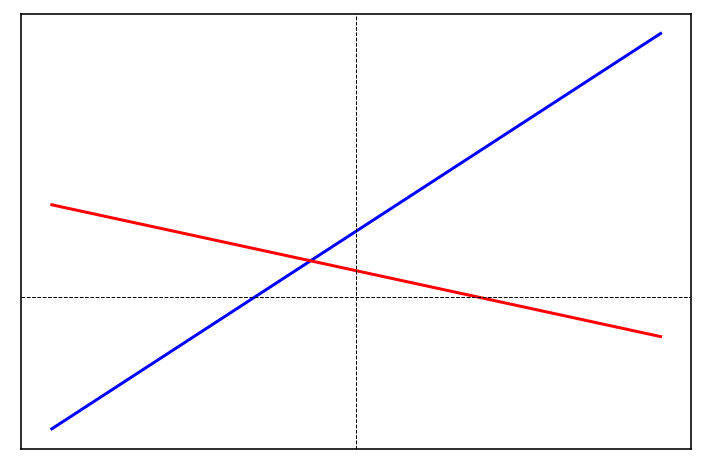
Unique Solution

Geometrically, a system with a unique solution is represented by two non-parallel lines:

Assuming for the moment that \(\displaystyle a_{1}\) and \(\displaystyle a_{2}\) are non-zero, we have a unique solution if and only if the two lines are not parallel:

\[ \begin{equation*} \cfrac{b_{1}}{a_{1}} \neq \cfrac{b_{2}}{a_{2}} \Longrightarrow a_{1} b_{2} -a_{2} b_{1} \neq 0 \end{equation*} \]

This is the same as stating that the following determinant should be non-zero:

\[ \begin{equation*} \begin{vmatrix} a_{1} & b_{1}\\ a_{2} & b_{2} \end{vmatrix} \neq 0 \end{equation*} \]

This is the geometric argument for introducing determinants. Notice that the expression \(\displaystyle a_{1} b_{2} -a_{2} b_{1}\) will work even when one or more coefficients are zero. If the determinant turns out to be zero, then we have two case.

No solution

Geometrically, a system with no solution is represented by two parallel lines that are distinct from each other:

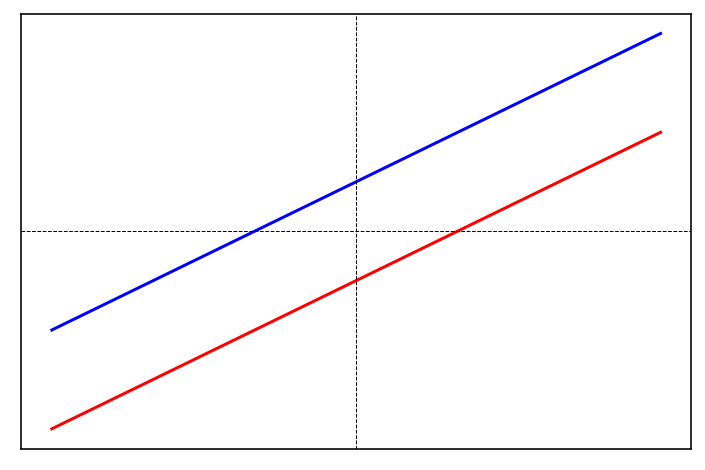
In this case, the slopes of the two equations are the same, but the intercepts are different:

\[ \begin{equation*} \cfrac{a_{1}}{a_{2}} =\cfrac{b_{1}}{b_{2}} \neq \cfrac{c_{1}}{c_{2}} \end{equation*} \]

Infinite Solutions

Geometrically, both equations correspond to the same line:

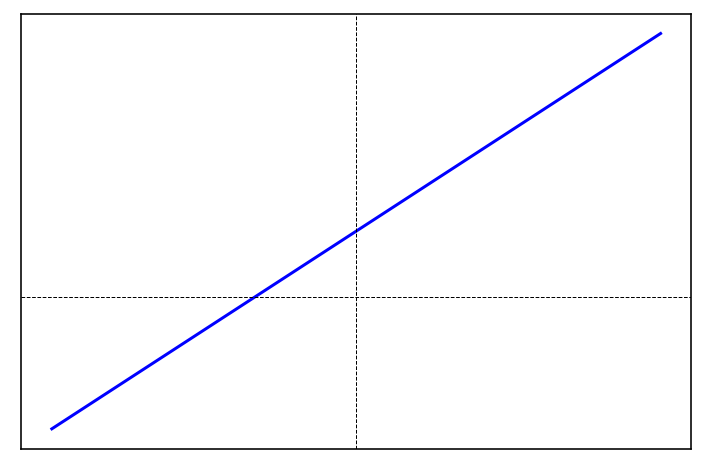
In this case, one equation is just a multiple of the other:

\[ \begin{equation*} \cfrac{a_{1}}{a_{2}} =\cfrac{b_{1}}{b_{2}} = \cfrac{c_{1}}{c_{2}} \end{equation*} \]