Problem-6
Question
When is the determinant of a \(2\times 2\) matrix equal to \(0\)? Geometrically, what does it mean?
Hint
See if you are able to find any patterns by studying these two determinants. \[ \begin{vmatrix} 1 & 2\\ 2 & 4 \end{vmatrix}, \begin{vmatrix} 3 & 9\\ 7 & 21 \end{vmatrix} \] For the geometric part, study the system \(Ax = 0\).
Solution
Algebra
Let \(A = \begin{bmatrix}a & b\\c & d\end{bmatrix}\). Determinants can be represented in this way: \[ \begin{equation*} \begin{vmatrix} a & b\\ c & d \end{vmatrix} =ad-bc \end{equation*} \]
The notation followed in this course is:
\[ \begin{equation*} det\left(\begin{bmatrix} a & b\\ c & d \end{bmatrix}\right) =ad-bc \end{equation*} \]
Now, the above expression gives the determinant of an arbitrary \(2 \times 2\) matrix. The determinant is zero when \(ad - bc = 0\). If \(ad-bc=0\), then one row/column is a multiple of the other row/column. To see why, consider the following steps. \[ \begin{equation*} ad=bc\Longrightarrow \cfrac{a}{b} =\cfrac{c}{d} =k\Longrightarrow a=kb,\ c=kd \end{equation*} \]
\[ \begin{equation*} ad=bc\Longrightarrow \frac{a}{c} =\frac{b}{d} =k\Longrightarrow a=kc,\ b=kd \end{equation*} \]
To keep things simple, we have implicitly used the fact that \(b, c, d \neq 0\) when dividing by these numbers, but the general result holds even if these numbers are zero. If this is still unclear, here is an alternative representation of these two cases:
Rows are multiples of each other: \[ \begin{vmatrix} r_1 & r_2\\ kr_1 & kr_2 \end{vmatrix} = 0 \] Columns are multiples of each other: \[ \begin{vmatrix} c_1 & kc_1\\ c_2 & kc_2 \end{vmatrix} = 0 \] Note that \(k\) can also be zero.
Geometry
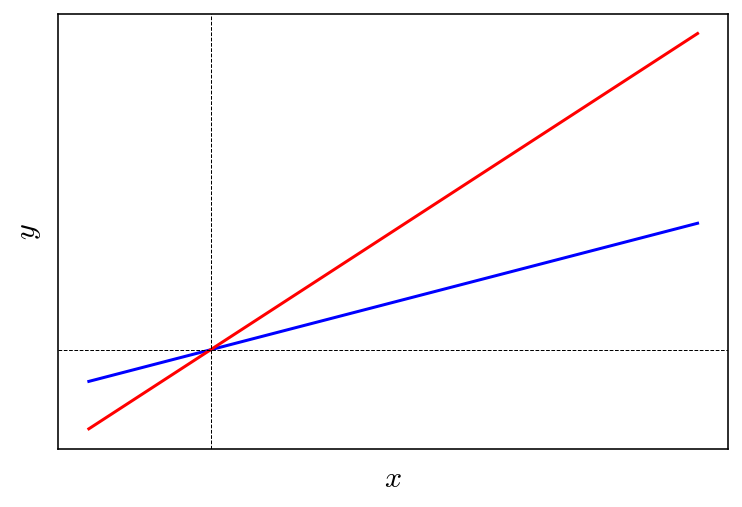
Geometrically, we can associate each row of the matrix to one line in the plane. The equations for these lines are \(ax + by = 0\) and \(cx + dy = 0\). These two lines pass through the origin. If one row is a multiple of the other, it means that both equations represent the same line. We can therefore conclude that the determinant of a \(2 \times 2\) matrix is non-zero if and only if the lines represented by the two rows are distinct.