Problem-2

Question

What happens if we scale every equation of a system of linear equations by a non-zero constant \(c\)? Answer this both algebraically and geometrically.

Hint

Take two simple equations in two variables. Multiply the LHS and RHS of both equations by \(2\) and observe what happens.

Solution

Scaling an equation by a non-zero \(c\) does not change the equation. For example:

\[ \begin{equation*} \begin{aligned} c\cdot ( 2x+3y+5z) & =c\cdot 10\\ c\cdot ( x-y+z) & =c\cdot 15\\ c\cdot ( x+z) & =c\cdot 25 \end{aligned} \ \ \leftrightarrow \ \ \begin{aligned} 2x+3y+5z & =10\\ x-y+z & =15\\ x+z & =25 \end{aligned} \end{equation*} \]

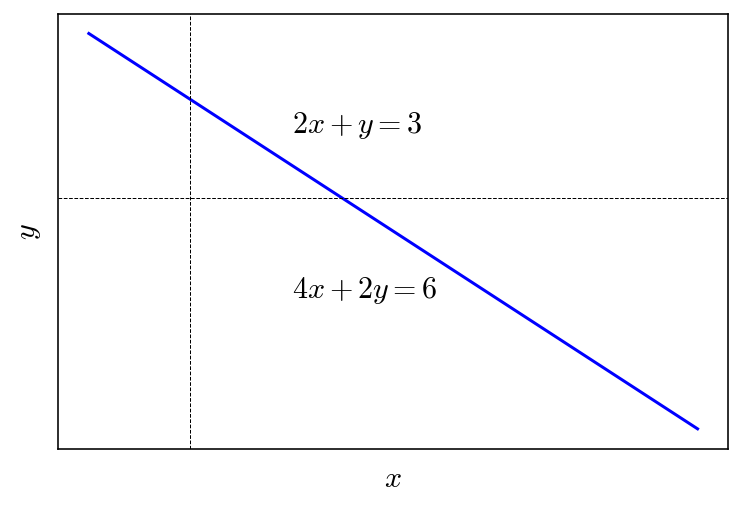
Geometrically, the line doesn’t change as a result of scaling. Consider the line \(2x + y = 3\). If we scale this by \(2\), we get \(4x + 2y = 6\), which is essentially the same line.