PPA-5
Question
Write a program to realize the equation of a line given 2 points \((x_1,y_1)\) and \((x_2,y_2)\) in 2D space. The input is in 5 lines where, the first, second, third, and fourth lines represent \(x_1\), \(y_1\), \(x_2\), and \(y_2\) respectively. The fifth line corresponds to \(x_3\). Determine \(y_3\) using the equation of a straight line as given below:
\[ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \]
The output should be “Vertical Line” if the line is vertical. In other cases, the output should be 2 lined, where the first line is the value of \(y_3\) and the second line indicates whether the slope of the line is positive, negative or zero. Print “Positive Slope”, “Negative Slope” or “Horizontal Line” accordingly.
Note that all inputs are to be processed as real numbers.
Hint
There are two aspects to this problem. One is mathematical, the other is computational. First, try to figure out the mathematical part. The questions you have to ask yourself are the following:
- For what collection of points does the line joining them become a vertical line?
- If a line is not vertical, then how does one compute the slope?
- What is the slope of a horizontal line?
Once you have answered these questions, you have all the ingredients necessary to solve the problem computationally. Some of the steps in the computational process:
- Accept inputs as real numbers. You know how to do this from PPA-2.
- Calculate the slope.
- Find the y-coordinate of the point.
There are important details that have been deliberately left out of this hint. These are for you to fill in.
Solution
For the mathematical part, refer to the image given below:
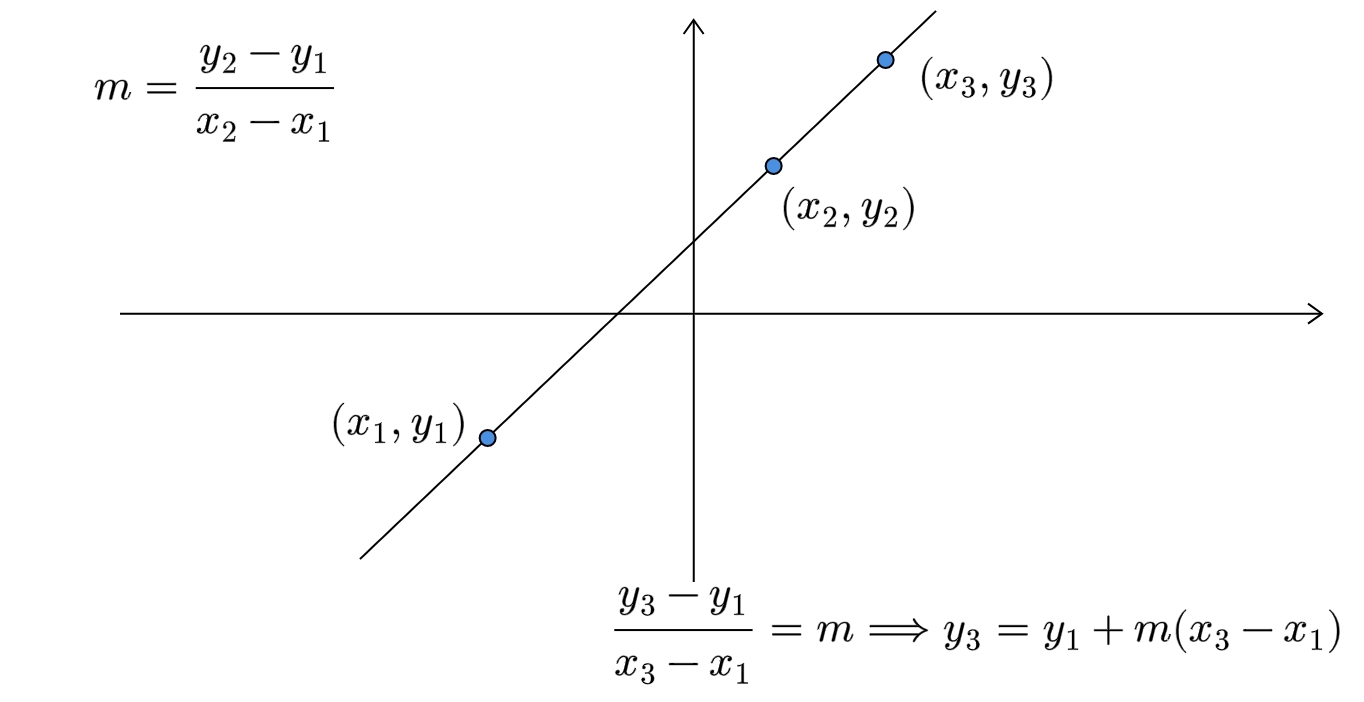
The slope of a vertical line is undefined. A line is vertical if the x-coordinates of the two points are the same, that is, when \(x_1 = x_2\). This gives us the first if-condition.
x1, y1 = float(input()), float(input())
x2, y2 = float(input()), float(input())
x3 = float(input())
if x1 != x2:
m = (y2 - y1) / (x2 - x1) # m is the slope
y3 = y1 + m * (x3 - x1)
print(y3)
if m == 0:
print('Horizontal Line')
elif m > 0:
print('Positive Slope')
else:
print('Negative Slope')
else:
print('Vertical Line')