Unsupervised Learning - Clustering - K-means/Kernel K-means

Note

Feedback/Correction: Click here!.

Introduction to Clustering

Clustering represents an essential method in unsupervised machine learning aimed at grouping similar objects into clusters, thereby revealing inherent structures within the data for exploratory analysis or serving as a preprocessing step for subsequent algorithms.

Our primary objective is to partition a set of \(n\) datapoints into \(k\) clusters.

Notation: \[ \mathbf{X}=\{\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_n \} \quad \mathbf{x}_i \in \mathbb{R}^d \] \[ S = \{\mathbf{z} \quad \forall \mathbf{z} \in \{1, 2, \ldots k\}^n \} \] \[ \boldsymbol{\mu} _k = \frac{\displaystyle \sum _{i = 1} ^{n} {\mathbf{x}_i \cdot \mathbb{1}(z_i=k)}}{\displaystyle \sum _{i = 1} ^{n} {\mathbb{1}(z_i=k)}} \]

Where:

\(\mathbf{x}_i\) denotes the \(i^{th}\) datapoint.
\(z_i\) denotes the cluster indicator of \(\mathbf{x}_i\).
\(\boldsymbol{\mu}_{z_i}\) denotes the mean of the cluster with indicator \(z_i\).
\(S\) represents the set of all possible cluster assignments. It is important to note that \(S\) is finite (\(k^n\)).

Goal: \[ \min _{\mathbf{z} \in S} \sum _{i=1} ^{n} {|| \mathbf{x}_i - \boldsymbol{\mu} _{z_i} ||}^2 \]

However, the manual solution to this optimization problem is classified as an NP-Hard problem, which necessitates considering alternative approaches to approximate its solution due to computational constraints.

K-means Clustering (Lloyd’s Algorithm)

Lloyd’s Algorithm, popularly known as the k-means algorithm, offers a widely utilized and straightforward clustering method that segregates a dataset into \(K\) predetermined clusters by iteratively computing the mean distance between the points and their cluster centroids.

The Algorithm

The algorithm proceeds as follows:

Step 1: Initialization: Randomly assign datapoints from the dataset as the initial cluster centers.

Step 2: Reassignment Step: \[ z _i ^{t} = \underset{k}{\arg \min} {|| \mathbf{x}_i - \boldsymbol{\mu} _{k} ^t ||}_2 ^2 \hspace{2em} \forall i \]

Step 3: Compute Means: \[ \boldsymbol{\mu} _k ^{t+1} = \frac{\displaystyle \sum _{i = 1} ^{n} {\mathbf{x}_i \cdot \mathbb{1}(z_i^t=k)}}{\displaystyle \sum _{i = 1} ^{n} {\mathbb{1}(z_i^t=k)}} \hspace{2em} \forall k \]

Step 4: Loop until Convergence: Repeat steps 2 and 3 until the cluster assignments do not change.

Convergence of K-means Algorithm

The convergence of K-means algorithm with respect to the objective is established by considering the following points:

The set of all possible cluster assignments \(S\) is finite.
The objective function value strictly decreases after each iteration of Lloyd’s Algorithm. \[ F(z_1^{t+1}, z_2^{t+1}, \ldots, z_n^{t+1}) < F(z_1^{t}, z_2^{t}, \ldots, z_n^{t}) \]

Moreover, a smarter initialization of K-means can improve the likelihood of converging to a good cluster assignment with a reduced number of iterations. Although the final assignment may not necessarily represent the global optima of the objective function, it is practically satisfactory as the objective function strictly decreases with each reassignment.

Considering the finiteness of the number of possible assignments (\(k^n\)), convergence of the algorithm is guaranteed.

Alternate Explanation: The convergence of the K-means algorithm is ascertained by its iterative nature, which minimizes the sum of squared distances between points and their cluster centroids—a convex function possessing a global minimum. The algorithm, under mild assumptions regarding the initial cluster means, reaches its convergence point, making it a dependable tool for clustering.

Nature of Clusters Produced by K-means

Let \(\boldsymbol{\mu}_1\) and \(\boldsymbol{\mu}_2\) denote the centroids of the clusters \(C_1\) and \(C_2\), respectively.

For \(C_1\), \[\begin{align*} {|| \mathbf{x} - \boldsymbol{\mu} _{1} ||}^2 &\le {|| \mathbf{x} - \boldsymbol{\mu} _{2} ||}^2 \\ \therefore \mathbf{x}^T(\boldsymbol{\mu} _2 - \boldsymbol{\mu} _1) &\le \frac{||\boldsymbol{\mu} _2||^2 - ||\boldsymbol{\mu} _1||^2}{2} \hspace{2em} \forall \mathbf{x} \end{align*}\]

The above equation takes the form of \(\mathbf{x}^T(w)<c\), indicating a linear separator or half-space. As a result, our resulting partition of the region represents an intersection of multiple half-spaces, commonly known as a Voronoi Partition.

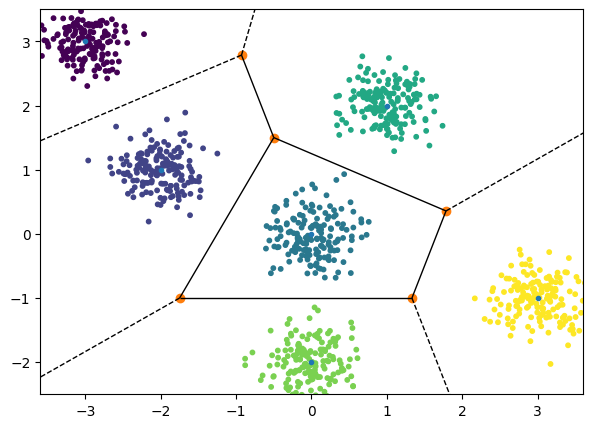
However, the standard k-means algorithm may not perform effectively when the underlying clusters in the dataset possess a non-linear structure. In such cases, alternative methods like Kernel K-means or Spectral Clustering can be employed to enhance clustering accuracy. Nonetheless, a detailed exploration of these methods is beyond the scope of this course.

Smart Initialization - K-means++

The concept of K-means++ involves selecting centroids that are maximally distant from each other.

Step 1: Randomly select \(\boldsymbol{\mu} _1 ^0\) from the dataset.
Step 2: For \(l \in \{2, 3, \ldots, k\}\), choose \(\boldsymbol{\mu} _l ^0\) probabilistically proportional to the score(\(S\)), where \(S\) is defined as follows: \[ S(\mathbf{x}_i) = \min _{\{j=1, 2, \ldots, l-1\}} {|| \mathbf{x}_i - \boldsymbol{\mu} _{j} ^0 ||}^2 \quad \forall \mathbf{x}_i \in \mathbf{X} \] The probabilistic aspect of the algorithm provides an expected guarantee of optimal convergence in K-means. The guarantee is given by: \[ \mathbb{E} \left[ \sum _{i=1} ^{n} {|| \mathbf{x}_i - \boldsymbol{\mu} _{z_i} ||}^2 \right ] \le O(\log k) \left [ \min _{\{z_1, z_2, \ldots, z_n\}} \sum _{i=1} ^{n} {|| \mathbf{x}_i - \boldsymbol{\mu} _{z_i} ||}^2 \right ] \] where \(O(\log k)\) is a constant of order \(\log k\).
Step 3: Once the centroids are determined, we proceed with our usual Lloyd’s Algorithm.

Choice of K

A prerequisite for K-means is determining the number of clusters, denoted as \(k\). However, what if the value of \(k\) is unknown?

If we were to choose \(k\) to be equal to \(n\): \[ F(z_1, z_2, \dots, z_n) = \sum _{i=1} ^{n} {|| \mathbf{x}_i - \boldsymbol{\mu} _{z_i} ||} ^2 = 0 \] However, as having as many clusters as datapoints is undesirable, we aim to minimize \(k\) while penalizing large values of \(k\). \[ \underset{k}{\arg \min} \left [ \sum _{i=1} ^{n} {|| \mathbf{x}_i - \boldsymbol{\mu} _{z_i} ||} ^2 + \text{Penalty}(k) \right ] \] Two common criteria for making the above argument are:

\(\text{\textcolor{blue}{Akaike Information Criterion}}\): \(\left [ 2K - 2\ln(\hat{\mathcal{L}}(\theta ^*)) \right ]\)
\(\text{\textcolor{blue}{Bayesian Information Criterion}}\): \(\left [ K\ln(n) - 2\ln(\hat{\mathcal{L}}(\theta ^*)) \right ]\)

However, detailed elaboration of these criteria is beyond the scope of this course.